Math solver for Science & Eng.
Simpler than Python or MATLAB; No programming, just math.
Start for free with a quick registration and use our numerical solver for common coursework tasks, student projects, and research.
Explore our sample programs that demonstrate the simple input syntax and rich solution reports. The solution reports include statistical analysis and visual charts—making results easy to interpret and apply.
Our internal algorithms have been widely adopted by STEM faculties at universities worldwide. Students and professionals value the application's simplicity and the depth of its solution reports.
Getting started is easy with these steps:
Click the Login button in the menu, then select the Register tab
Click the Solver button in the menu and run the samples
Enter your math problems to get detailed solution reports
To go beyond, consider one of our affordable paid licenses. You'll scale your capabilities to address larger problems, unlock advanced features, and benefit from higher limits. Plus, you'll gain access to our enhanced Windows desktop package.
Solver Examples |
 |
Explore these examples to learn the simple problem entry syntax. Each example popup shows the problem input in the left panel and the solution output in the right panel.

Equations Solver |
 |
When solving nonlinear equations—whether a single equation or a system—write each equation so it equals 0 (root-finding form) and provide an initial guess for each variable. In other words, express each equation as 𝑓(𝑥)=0 and supply an initial guess for every nonlinear variable.
Here's a quick example showing how to set up and enter the data for solving two simultaneous nonlinear equations:

The unknown variables are x and y.
Below are the root expressions, each corresponding to one of the unknowns, along with initial estimates—both set to 1.
Note that any part of a line starting with # is treated as a user comment.
It's ignored during evaluation and has no effect on the calculations
You can also define any number of auxiliary expressions to help simplify long formulas. In the example below, we define a as an auxiliary expression—meaning it's treated as a separate, explicit variable that other expressions can reference. You don't need to provide initial guesses for auxiliary explicit variables—they're automatically computed from the nonlinear variables with provided initial guesses.
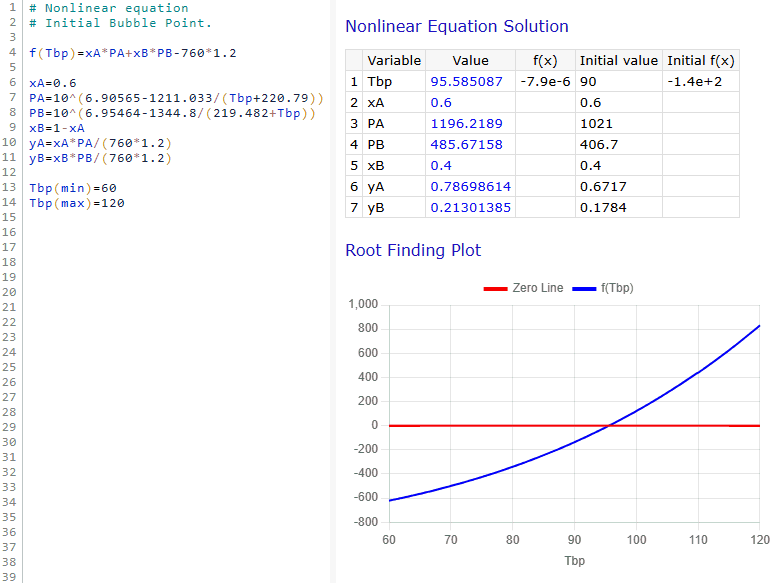
When solving a single nonlinear equation—even if you include as many explicit helper variables and expressions as you like—the way you set the starting values is a bit different. Instead of giving just one guess, you need to provide both a minimum and a maximum estimate for the variable.
Take a look at this example where we solve a nonlinear equation to find the value of V.
When solving multiple linear equations, you can enter them in the standard format—just as you'd normally write them. There's no need to rearrange the equations or provide any initial guesses. Simply ensure that all the equations are truly linear.
Here's an example of three linear equations being solved simultaneously:

The following equations should be entered into PolymathPlus to solve the system described above:
Differential Equations |
 |
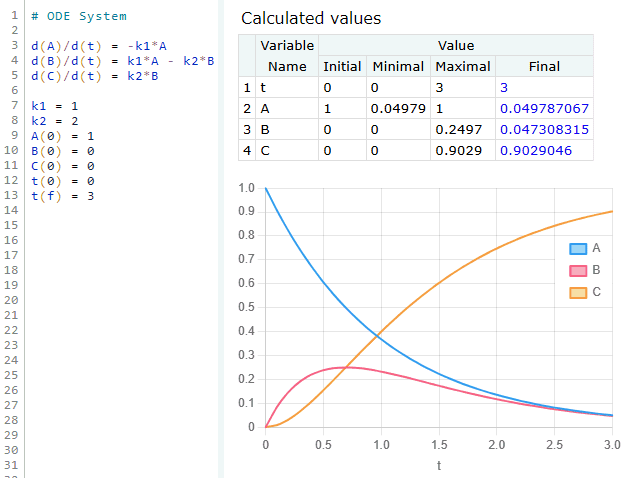
PolymathPlus is designed to solve systems of simultaneous initial value problems (IVPs) involving first-order ordinary differential equations (ODEs).
Higher-order differential equations can be transformed into systems of first-order equations using standard mathematical techniques. Likewise, partial differential equations (PDEs) can be converted into ODEs for numerical solution using methods such as the method of lines.
Each equation in PolymathPlus must be written in first-order form, where the derivative of a dependent variable is isolated on the left-hand side and expressed as an algebraic function of independent and dependent variables. This structure ensures compatibility with the program's numerical solvers.
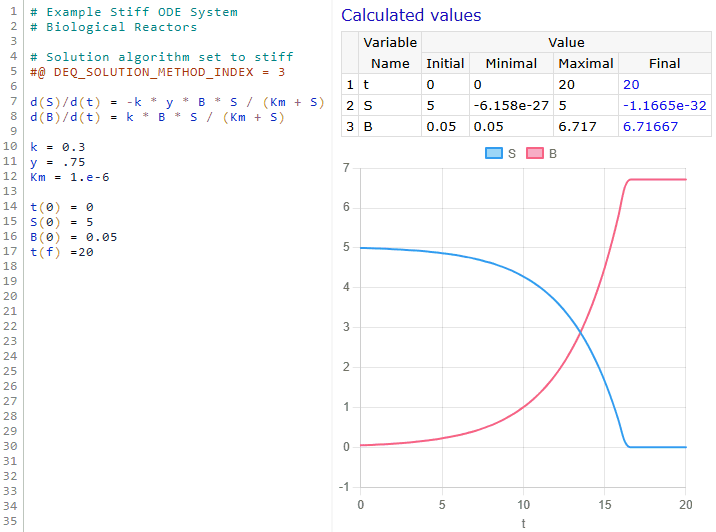
Consider this set of ordinary differential equations to be solved:

Given the initial conditions x0 = 1 and y0 = 4 at t0 = 0, with integration ending at tf = 1, the following should be entered:
You can also use either of the following two compatible syntax formats for the same problem:
The output shows a table of results along with an integration chart.

In addition to differential equations, PolymathPlus allows users to define explicit variables—algebraic expressions that depend on differential variables, the independent variable, and/or other explicit variables, provided no circular dependencies exist. These variables are computed directly from known values and can be used to simplify equations, define intermediate results, or support the overall structure of the model.
The example below illustrates a typical input format for solving a system of ordinary differential equations (ODEs) in PolymathPlus, including the use of explicit variables.
Curve Fitting |
 |
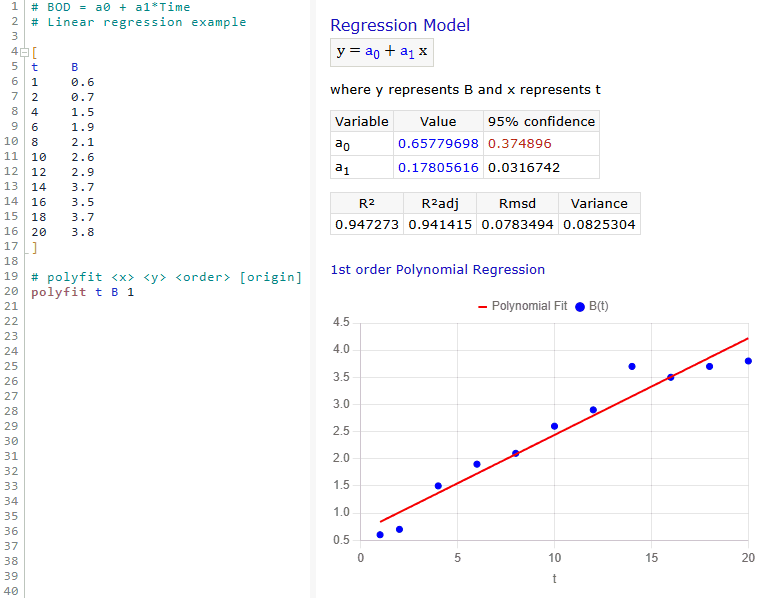
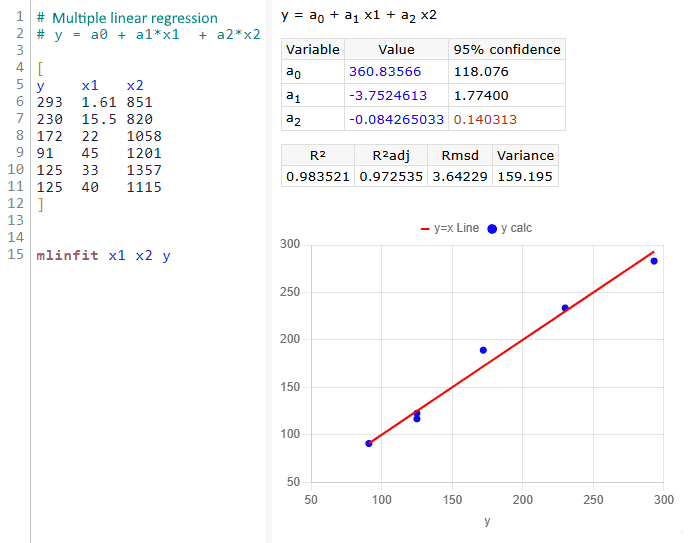
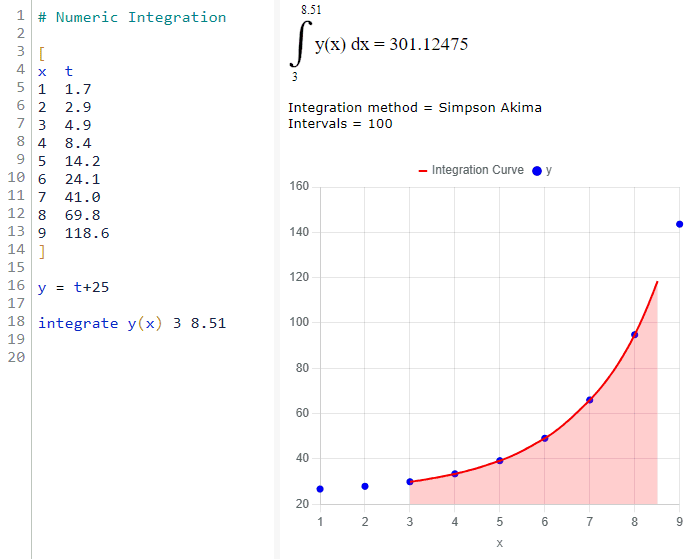
PolymathPlus supports curve fitting for linear, polynomial, multi-linear, and nonlinear regression. The report evaluates model variables, generates a regression chart and residual plots, and provides statistics on model accuracy.
Below is an example of the data entry required to solve a linear regression model for a given set of data points.
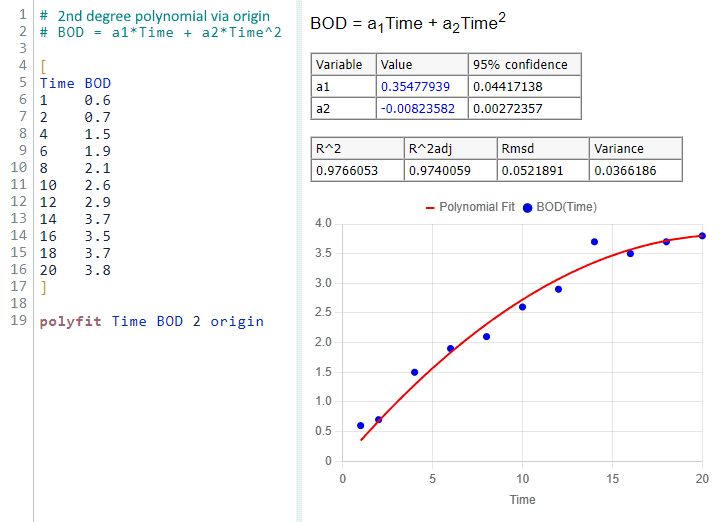
This example demonstrates a polynomial regression model of order 1 (i.e., linear regression), which finds the best-fitting linear equation for the given data points.

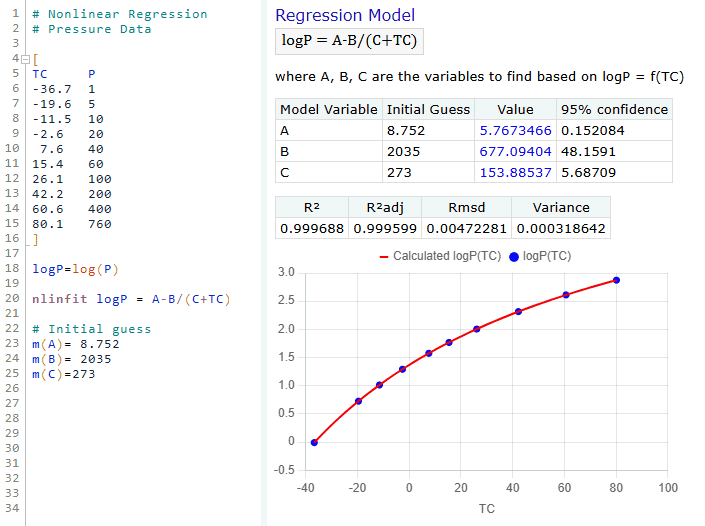
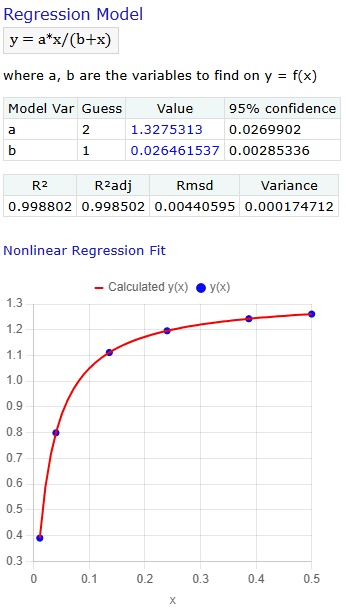
Below is an example of a data entry for solving nonlinear regression model for a given set of data points. The model variables to be found are a and b, for which we should also provide an initial guess.
and the solution becomes:
Pricing |
 |
Our free license is powerful and available at no cost. Get started with it by simply registering and logging in. For advanced users, affordable paid licenses with expanded capabilities are also available, starting at just $15 annually.
The following table lists some of the program key capacities and features per license.
| Capacity & Features | Free | Std | Pro |
| Online storage capacity | 5 | 100 | ∞ |
| Nonlinear equations | 5 | 10 | 100 |
| Differential equations | 5 | 10 | 2000 |
| Supporting auxiliary variables | 10 | 50 | 2000 |
| Regression data points | 20 | 100 | ∞ |
| Regression model variables | 5 | 10 | ∞ |
| Intermediate data points table | 50 | 300 | 1000 |
| Solver requests per month | 100 | ∞ | ∞ |
| Online solver | ✅ | ✅ | ✅ |
| Windows desktop application | ✅ | ✅ | |
| Dynamic charts | ✅ | ✅ | |
| Advanced tools | ✅ | ||
| Annual Cost excluding sales tax (USD) | Free | $15 🛒 | $50 🛒 |
Users can purchase individual Student or Pro licenses through their online profile page.
| Site License | Annual Cost | |
| $370 | per 50 users | |
| $450 | per 100 users | |
| $1250 | per 50 users | |
| $1500 | per 100 users | |
Institutions with site licenses may install the desktop version on their public computers.
To initiate the registration of a new site, please reach out to us and provide the following details:
| Detail | Example | |
| 1. | Site name | Arizona State University |
| 2. | IT contact email | john123@asu.edu |
| 3. | Backup email | abra2759@asu.edu |
| 4. | Email extension/s | @asu.edu, @student.asu.edu |
| 5. | Site Address | ABC College 123 University Avenue College Town, CA 98765 United States |
Support and FAQ |
 |
Our support team typically replies to account, licensing, and common troubleshooting requests within one business day. For technical questions, enhancement requests, or bug reports, email admin@polymathplus.org with a brief description and any screenshots; for licensing or purchase inquiries, please include the account email and any relevant site details.
Below you'll find common support questions and answers:
About Us |
 |
PolymathPlus began as a Windows desktop application and expanded its offerings to include an online web application. Our passion and dedication drive us to continually innovate and refine our solutions. We are committed to providing a top-notch numerical solver package to tackle mathematical challenges with ease and confidence.
 |
admin@polymathplus.org
sales@polymathplus.org |
 |
+1 530 405 9303 |
| +995 557 440 981 | |
| Pre-scheduled calls only 08:00-10:00 AM ET |
|
 |
Maintenance Status |
The development of our software had been encouraged by CACHE - The Computer Aids for Chemical Engineering Education Corporation, as part of the American Institute of Chemical Engineers.
Drawing from more than 25 years of software development and extensive research in numerical packages, we have crafted the new PolymathPlus package. We maintain ties with many US-based universities and colleges, as well as institutions across other regions worldwide.
Deliver the premier user-friendly, advanced math solver—accessible and affordable worldwide—the first choice for learners, professionals, and enthusiasts.
Research |
 |
Our research is dedicated to advancing numerical methods and optimization techniques to strengthen the capabilities of PolymathPlus. The following key research areas highlight their potential impact across disciplines commonly applied in science and engineering, particularly in design, modeling, and control.
Optimization solvers find a function's minimum or maximum.
Engineers often apply classical numerical methods like Gradient Descent, Conjugate Gradient, BFGS, and L-BFGS to solve these problems efficiently. These algorithms improve convergence and reduce computation time, especially for smooth, differentiable functions and large-scale systems.
To tackle Constrained optimization problems (where seeking the optimal maximum or minimum of a function while satisfying variable constraints), engineers use classical methods like the Augmented Lagrangian approach, Generalized Reduced Gradient (GRG), and Karush-Kuhn-Tucker (KKT) conditions. These techniques are designed to handle complex systems with multiple constraints, ensuring feasible and efficient solutions
Solving partial differential equations is central to modeling physical phenomena in engineering and science — from heat transfer and fluid dynamics to structural mechanics and electromagnetics. Robust numerical algorithms are developed to tackle these equations efficiently and accurately.
Common approaches include finite difference methods for structured grids, finite element methods for complex geometries, and spectral methods for high-precision solutions. These techniques enable engineers to simulate and analyze systems governed by PDEs across a wide range of applications.
The Simplex method solves linear programming problems by moving along the edges of feasible solutions to find the optimal one.
Enhancing Simplex algorithms with advanced pivot rules, degeneracy handling, and dual simplex implementations to handle large-scale linear optimization problems more efficiently. Research includes interior-point methods and revised simplex algorithms for improved numerical stability.
Developing specialized solvers for boundary value problems and parameter optimization in ordinary differential equations, including shooting methods and multiple shooting techniques.
Combining advanced regression techniques with ODE solvers for better model fitting in dynamic systems, enabling parameter estimation in complex mathematical models.
Chebyshev and Fourier transformations are mathematical tools used to represent functions using orthogonal basis sets. They enhance numerical solvers for discrete data, improving accuracy and computational efficiency in interpolation and approximation. These transformations also enable advanced solvers by replacing discrete data with continuous function representations.
These research efforts represent our ongoing commitment to improving computational mathematics. While we work to incorporate these advancements into PolymathPlus, we aim to provide users with reliable and efficient tools for solving complex mathematical problems.
Solution Reports |
 |
Below are sample reports generated by solving PolymathPlus programs. The input for each program is shown at the top of every report. Each group features example problems and their corresponding solution reports.
Terms and Conditions PolymathPlus does not warrant that the functions contained in the program will meet your requirements or that the operation of the program will be uninterrupted or error-free. In no event will PolymathPlus or its distributors or their dealers be liable to you for any damages, including any lost profit, lost savings, or other incidental or consequential damage. Please read the Terms of Service (TOS) below for further details.